v and T as state variables
In some cases it is convenient to use molar quantities and mole fractions in the formulation of an EOS. In that case, a slightly different method can be used to calculate ![]() . Let us start with a slightly different form of Equation (53)
. Let us start with a slightly different form of Equation (53)
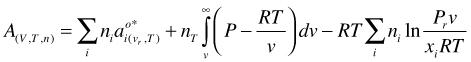
(64)
and make it molar by dividing by the total number of moles nT
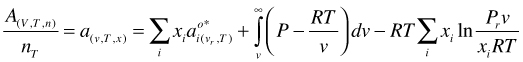
(65)
It is obvious that:
![]()
(66)
Here the molar Helmoltz free energy a(v,T,x) is a function of v, T, and x instead of V, T, and n. Now instead of differentiating the left side of Equation (66), we use the right hand side and apply the product rule
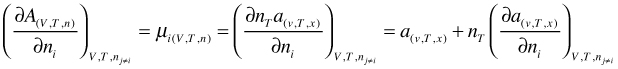
(67)
Because x as well as v (V is the relevant thermodynamic variable and v=V/nT) are functions of n we have to apply the general chain rule for the differentiation:
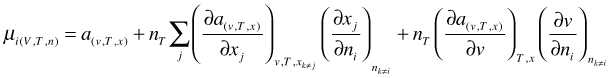
(68)