In general the change of Gibbs free energy for a phase equilibrium (ΔG(P, T)) at pressure P and temperature T is given by
where νi is the stoichiometric coefficient of the i th phase component, k is the total number of phase components involved in the equilibrium and Gi is the Gibbs free energy of the i th phase component at P and T.
Further consideration requires the definition of standard states and reference conditions. Solids are considered to be in standard state if they are of pure end member composition (pure phase component) and reference conditions are 0.1 MPa and 298 K. Fluids are treated as pure hypothetical ideal gases at a reference pressure of 0.1 MPa (1 bar) and temperature T. ΔG(P, T) is then given by
where Δ designates an equivalent relationship for each parameter or function except for ΔV°S(P, T). In this case Δ designates only the change in volume of the pure solid phase components. The pressure dependence of the Gibbs free energy of the fluid phase components is incorporated in the equilibrium constant K(P, T):
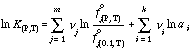
where f°j(P, T) is the fugacity of the j th pure fluid phase component, ν is total number of fluid phase components, and ai are the activities of the i th phase component.
In the case that the heat capacitiy of a phase is only available in intervals, the following relationship is used:
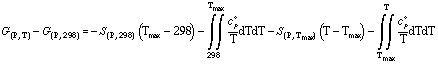
or in the case of a phase transition the following relationship is applied:
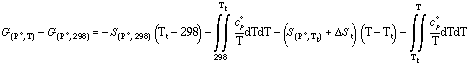
where
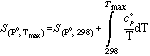
The molar volumes of solids at elevated pressure and temperature are evaluated with the compressibility coefficient β and the thermal expansion coefficient α.
The combination and integration with the assumption that α and β are not a function of pressure and temperature leads to:
Although α and β are treated as constants, this relationship mimics the real volume change as a function of pressure and temperature. With this equation the second integral of the main equation is calculated for n solid phase components involved in the phase equilibrium:
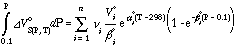
The last three terms of the main equation can be combined to form the reduced equilibrium constant ln Kred
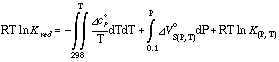
which leads to:
Evaluation of the right hand side leads to the following conditions:
reactants stable 
equilibrium 
products stable
In evaluating the ln Kred term for each available experimental result, the heat capacities for all components, the molar volumes and the coefficients of the thermal expansion and compressibility of the solids are required. If any fluids are involved, their functions of state are also required. If mixed phases are considered, activity models must be taken into account. Lastly, some phases show phase transitions as a function of P and T, while others reveal a continuous change in the degree of order, all of which must be considered thermodynamically.
